GeoExamples - Roger Veciana

Shortest distance to a geometry in a specified direction using Python

Sat, 16 Aug 2014

Looking at this map, I wondered how to calculate which geometry in a set is the closest to a point in a given direction.

Usually, the problem is finding the closest geometry in general, which is easy using the distance function, but I couldn’t find a solution for this other.

So I put me this problem: Which is the closest country that I have at each direction, knowing my geographical coordinates?

All the source code is, as usual, at GitHub

The algorithm

The main idea is:

  1. Create an infinite line from the point towards the desired direction.
  2. Calculate the difference geometry between the line and each polygon
  • If the polygon and the line actually intersect, the result will be a multi-line. The first line length of the multi-line is the distance we are looking for

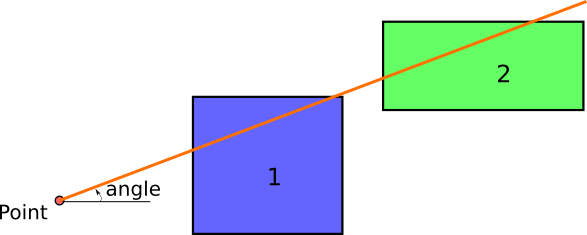
So this would be the initial situation:

And the distance to the polygon 1 would be calculated as:

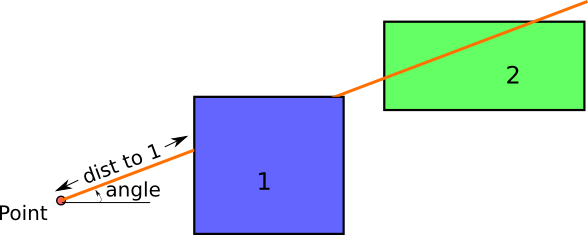
The main problem is how to calculate the difference between the two geometries, but fortunately, shapely comes with this function, so coding it is not so difficult:

from shapely.geometry import Polygon
from shapely.geometry import LineString
from math import cos
from math import sin
from math import pi

def closest_polygon(x, y, angle, polygons, dist = 10000):

    angle = angle * pi / 180.0
    line = LineString([(x, y), (x + dist * sin(angle), y + dist * cos(angle))])

    dist_min = None
    closest_polygon = None
    for i in range(len(polygons)):
        difference = line.difference(polygons[i])
        if difference.geom_type == 'MultiLineString':
            dist = list(difference.geoms)[0].length
            if dist_min is None or dist_min > dist:
                dist_min = dist
                closest_polygon = i



    return {'closest_polygon': closest_polygon, 'distance': dist_min}

if **name** == '**main**':

    polygons = []
    polygons.append(Polygon([(4, 2), (4, 4), (6, 4), (6, 2)]))
    polygons.append(Polygon([(7, 2), (7, 4), (9, 4), (9, 2)]))


    print closest_polygon(3, 3, 90, polygons)

  • The main section creates the two squares using shapely

  • The closest_polygon function calculates the closest polygon and its distance:

    • A LineString to the desired direction is calculated. The dist is in the units used by the polygons. An infinite line isn’t possible, so the distance must be larger than the further
    • For each of the polygons to analyze, the difference is calculated using the shapely difference method
    • Then, if the line and the polygon intersect (and the line is long enough), a MultilineString will be the result of the difference operation. The first String in the MultilineString is the one that connects our point with the polygon. Its length is the distance we are looking for
    The example schema, drawn with the script draw_closest.py

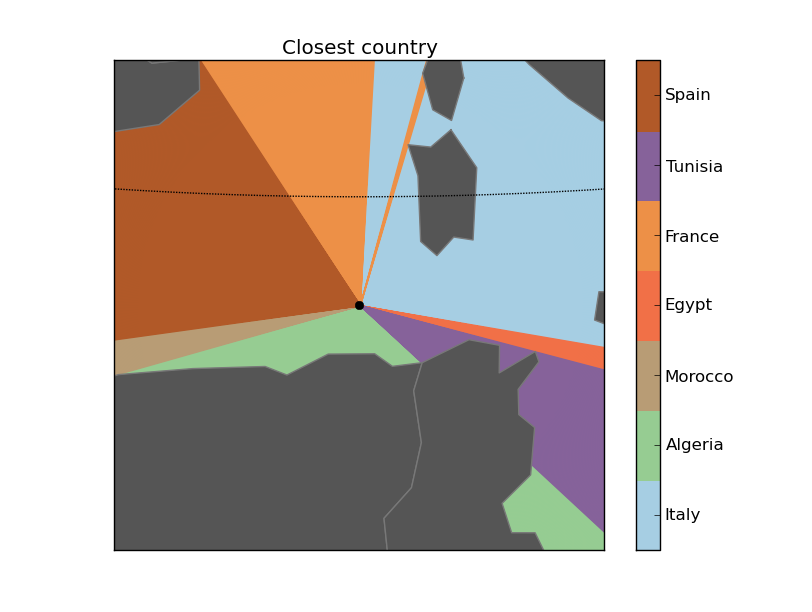
Calculating the closest country in each direction

After getting the formula for calculating the closest polygon, the next step would be using it for something. So:

 Which country do I have in all directions?

To create the script, some things have to be considered:

  • The projection should be azimuthal equidistant so the distances can be compared in all the directions from the given point
  • I’ve used the BaseMap library to draw the maps. I find it a bit tricky to use, but the code will be shorter

The script is used this way:

usage: closest_country.py [-h] [-n num_angles] [-o out_file] [-wf zoom_factor] lon lat

Creates a map with the closest country in each direction

 positional arguments:
   lon              The point longitude
   lat              The point latitude

 optional arguments:
   -h, --help       show this help message and exit
   -n num_angles    Number of angles
   -o out_file      Out file. If present, saves the file instead of showing it
   -wf zoom_factor  The width factor. Use it to zoom in and out. Use > 1 to
                    draw a bigger area, and <1 for a smaller one. By default is
                    1

For example:

 python closest_country.py -n 100 -wf 2.0 5 41

The code has some functions, but the main one is draw_map:

def draw_map(self, num_angles = 360, width_factor = 1.0):

    #Create the map, with no countries
    self.map = Basemap(projection='aeqd',
                lat_0=self.center_lat,lon_0=self.center_lon,resolution =None)
    #Iterate over all the angles:
    self.read_shape()
    results = {}
    distances = []
    for num in range(num_angles):
        angle = num * 360./num_angles
        closest, dist = self.closest_polygon(angle)
        if closest is not None:
            distances.append(dist)
            if (self.names[closest] in results) == False:
                results[self.names[closest]] = []

            results[self.names[closest]].append(angle)

    #The map zoom is calculated here,
    #taking the 90% of the distances to be drawn by default
    width = width_factor * sorted(distances)[
            int(-1 * round(len(distances)/10.))]

    #Create the figure so a legend can be added
    plt.close()
    fig = plt.figure()
    ax = fig.add_subplot(111)
    cmap = plt.get_cmap('Paired')


    self.map = Basemap(projection='aeqd', width=width, height=width,
                lat_0=self.center_lat,lon_0=self.center_lon,resolution =None)
    self.read_shape()

    #Fill background.
    self.map.drawmapboundary(fill_color='aqua')

    #Draw parallels and meridians to give some references
    self.map.drawparallels(range(-80, 100, 20))
    self.map.drawmeridians(range(-180, 200, 20))


    #Draw a black dot at the center.
    xpt, ypt = self.map(self.center_lon, self.center_lat)
    self.map.plot([xpt],[ypt],'ko')

    #Draw the sectors
    for i in range(len(results.keys())):
        for angle in results[results.keys()[i]]:
            anglerad = float(angle) * pi / 180.0
            anglerad2 = float(angle + 360./num_angles) * pi / 180.0
            polygon = Polygon([(xpt, ypt), (xpt + width * sin(anglerad), ypt + width * cos(anglerad)), (xpt + width * sin(anglerad2), ypt + width * cos(anglerad2))])
            patch2b = PolygonPatch(polygon, fc=cmap(float(i)/(len(results) - 1)), ec=cmap(float(i)/(len(results) - 1)), alpha=1., zorder=1)
            ax.add_patch(patch2b)


    #Draw the countries
    for polygon in self.polygons:
        patch2b = PolygonPatch(polygon, fc='#555555', ec='#787878', alpha=1., zorder=2)
        ax.add_patch(patch2b)

    #Draw the legend
    cmap = self.cmap_discretize(cmap, len(results.keys()))
    mappable = cm.ScalarMappable(cmap=cmap)
    mappable.set_array([])
    mappable.set_clim(0, len(results))
    colorbar = plt.colorbar(mappable, ticks= [x + 0.5 for x in range(len(results.keys()))])
    colorbar.ax.set_yticklabels(results.keys())

    plt.title('Closest country')

  • The first steps are used to calculate the closest country in each direction, storing the result in a dict. The distance is calculated using the closest_polygon method, explained in the previous section..

  • The actual map size is then calculated, taking the distance where the 90% of the polygons will appear. The width_factor can change this, because some times the result is not pretty enough. Some times has to much zoom and some, too few. Note that the aeqd i.e., Azimuthal Equidistant projection is used, since is the one that makes the distances in all directions comparable.

  • Next steps are to actually drawing the map

    • The sectors (the colors indicating the closest country) are drawn using the Descartes library and it’s PolygonPatch
    • The legend needs to change the color map to a discrete color map. I used a function called cmap_discretize, found here, to do it
    • The legend is created using the examples found in this cookbook

    Some outputs:

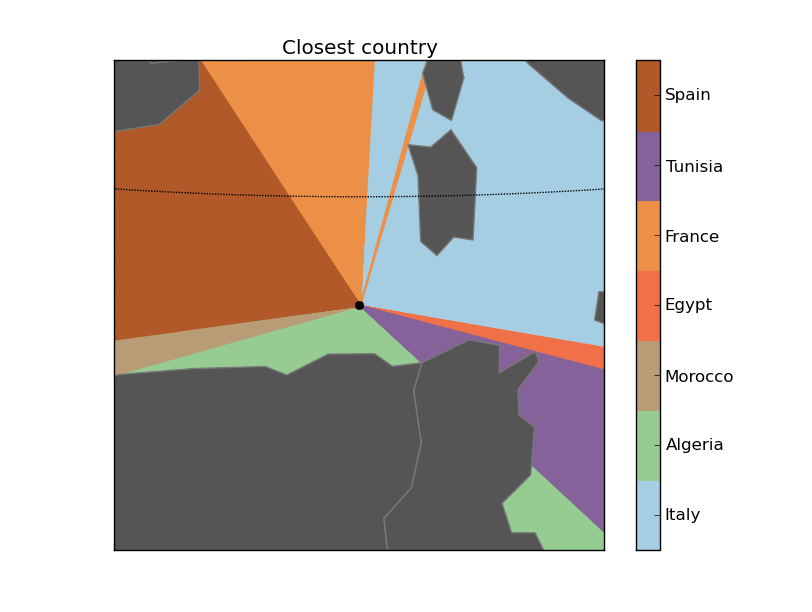
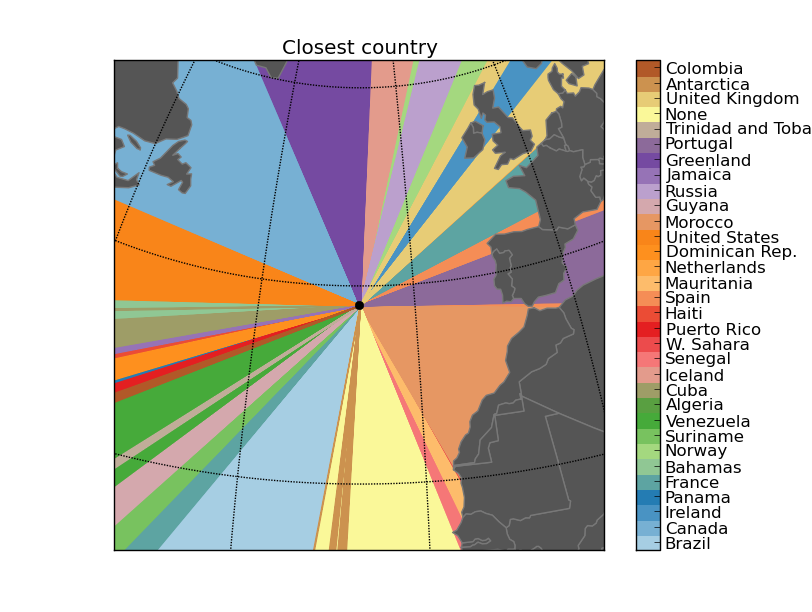
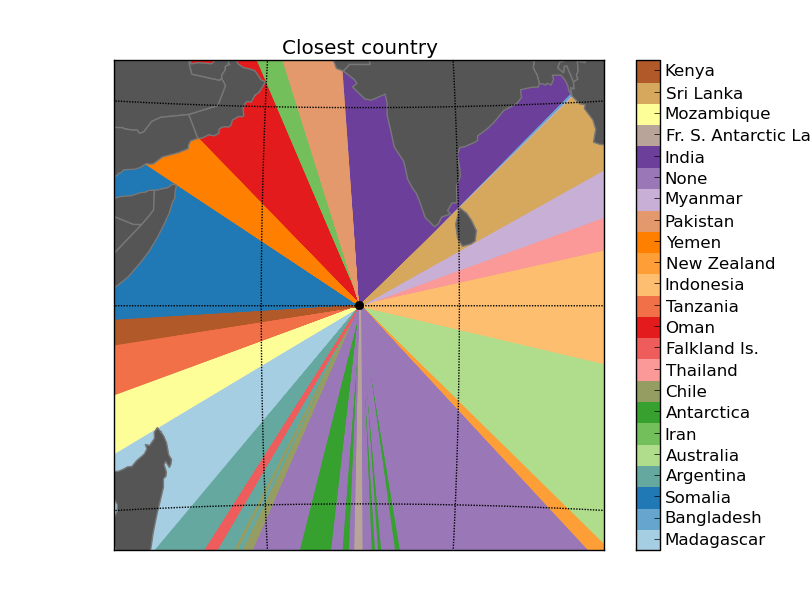
Next steps: What’s across the ocean

Well, my original idea was creating a map like this one, showing the closest country when you are at the beach. Given a point and a direction (east or west in the example), calculating the country is easy, and doing it for each point in the coast is easy too. The problem is that doing it automatic is far more difficult, since you have to know the best direction (not easy in many places like islands), which countries to take as the origin, etc.

An other good thing would be doing the same, but with d3js, since the point position could become interactive. I found some libraries like turfjs, shapely.js or jsts, but I think that they still don’t implement the difference operation that we need.

Basemap links